สัญลักษณ์ ใด ที่ แสดง ถึงขนาด ของแรง

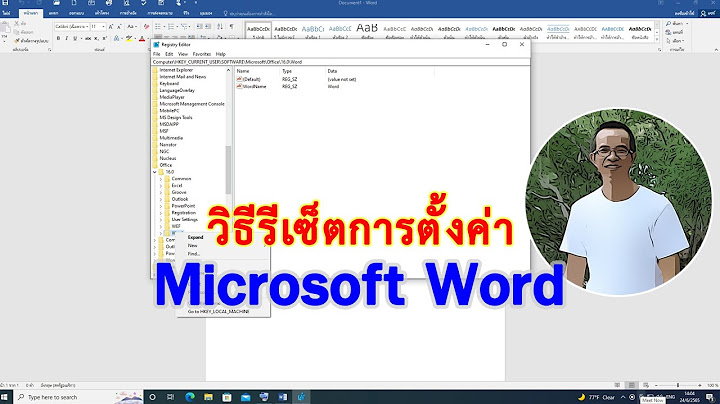
แรงสุทธิคือผลรวมเวกเตอร์ของแรงที่กระทำต่ออนุภาคหรือร่างกาย แรงสุทธิเป็นแรงเดี่ยวที่แทนที่ผลของแรงดั้งเดิมที่มีต่อการเคลื่อนที่ของอนุภาค มันทำให้อนุภาคเดียวกันเร่งเป็นกองกำลังทั้งหมดที่เกิดขึ้นจริงเหล่านั้นเข้าด้วยกันตามที่อธิบายกฎข้อที่สองของนิวตันของการเคลื่อนไหว

ในทางฟิสิกส์เป็นไปได้ที่จะกำหนดแรงบิดที่เกี่ยวข้องกับจุดของการใช้แรงสุทธิเพื่อให้มันรักษาการเคลื่อนที่ของไอพ่นของวัตถุภายใต้ระบบแรงเดิม แรงบิดที่สัมพันธ์กันของมันคือแรงสุทธิกลายเป็นแรงผลลัพธ์และมีผลเช่นเดียวกันกับการเคลื่อนที่แบบหมุนของวัตถุเมื่อแรงจริงทั้งหมดรวมกัน [1]เป็นไปได้ที่ระบบของกองกำลังจะกำหนดแรงที่เป็นผลลัพธ์ที่ปราศจากแรงบิด ในกรณีนี้แรงสุทธิเมื่อนำไปใช้กับแนวปฏิบัติที่เหมาะสมจะมีผลเช่นเดียวกันกับร่างกายเช่นเดียวกับแรงทั้งหมดที่จุดของการใช้งาน เป็นไปไม่ได้เสมอไปที่จะหาแรงที่เป็นผลลัพธ์ที่ปราศจากแรงบิด

วิธีแผนภาพสำหรับการเพิ่มกองกำลัง

Force คือปริมาณเวกเตอร์ซึ่งหมายความว่ามีขนาดและทิศทางและโดยปกติจะแสดงด้วยตัวหนาเช่นFหรือโดยใช้ลูกศรเหนือสัญลักษณ์เช่นฉ→{\ displaystyle \ scriptstyle {\ vec {F}}} $\scriptstyle {\vec F}$ .

ในทางกราฟิกแรงจะแสดงเป็นส่วนของเส้นตรงจากจุดของแอปพลิเคชันAไปยังจุดBซึ่งกำหนดทิศทางและขนาดของมัน ความยาวของส่วนABแสดงถึงขนาดของแรง

แคลคูลัสเวกเตอร์ได้รับการพัฒนาในช่วงปลายทศวรรษที่ 1800 และต้นทศวรรษที่ 1900 กฎสี่เหลี่ยมด้านขนานใช้สำหรับการเพิ่มขึ้นของกองกำลัง แต่วันตั้งแต่สมัยโบราณและมีการตั้งข้อสังเกตอย่างชัดเจนโดยกาลิเลโอและนิวตัน [2]

แผนภาพแสดงการเพิ่มของกองกำลัง ฉ→1{\ displaystyle \ scriptstyle {\ vec {F}} _ {1}} $\scriptstyle {\vec {F}}_{{1}}$ และ ฉ→2{\ displaystyle \ scriptstyle {\ vec {F}} _ {2}} $\scriptstyle \vec{F}_{2}$ . ผลรวมฉ→{\ displaystyle \ scriptstyle {\ vec {F}}} $\scriptstyle {\vec F}$ ของทั้งสองกองกำลังวาดเป็นเส้นทแยงมุมของสี่เหลี่ยมด้านขนานที่กำหนดโดยทั้งสองแรง

กองกำลังที่ใช้กับร่างกายส่วนขยายอาจมีจุดใช้งานที่แตกต่างกัน กองกำลังเป็นเวกเตอร์ที่ถูกผูกไว้และสามารถเพิ่มได้ก็ต่อเมื่อถูกนำไปใช้ที่จุดเดียวกัน แรงสุทธิที่ได้รับจากแรงทั้งหมดที่กระทำต่อร่างกายจะไม่รักษาการเคลื่อนที่เว้นแต่จะถูกนำไปใช้ที่จุดเดียวกันและด้วยแรงบิดที่เหมาะสมซึ่งสัมพันธ์กับจุดใหม่ของการใช้งานที่กำหนด แรงสุทธิของร่างกายที่กระทำ ณ จุดเดียวด้วยแรงบิดที่เหมาะสมเรียกว่าแรงและแรงบิดที่เป็นผลลัพธ์

Parallelogram ABCD

แรงเรียกว่าเวกเตอร์ที่มีขอบเขตซึ่งหมายความว่ามันมีทิศทางและขนาดและจุดของการประยุกต์ใช้ วิธีที่สะดวกในการกำหนดแรงโดยส่วนของเส้นจากจุดไปยังจุดB ถ้าเราแสดงพิกัดของจุดเหล่านี้เป็นA = (A x , A y , A z ) และB = (B x , B y , B z ) ดังนั้นเวกเตอร์แรงที่ใช้กับAจะถูกกำหนดโดย

ฉ=ข-ก=(ขx-กx,ขย-กย,ขz-กz).{\ displaystyle \ mathbf {F} = \ mathbf {B} - \ mathbf {A} = (B_ {x} -A_ {x}, B_ {y} -A_ {y}, B_ {z} -A_ {z }).} ${\mathbf {F}}={\mathbf {B}}-{\mathbf {A}}=(B_{x}-A_{x},B_{y}-A_{y},B_{z}-A_{z}).$

ความยาวของเวกเตอร์B - AกำหนดขนาดของFและกำหนดโดย

|ฉ|=(ขx-กx)2+(ขย-กย)2+(ขz-กz)2.{\ displaystyle | \ mathbf {F} | = {\ sqrt {(B_ {x} -A_ {x}) ^ {2} + (B_ {y} -A_ {y}) ^ {2} + (B_ { z} -A_ {z}) ^ {2}}}} $|{\mathbf {F}}|={\sqrt {(B_{x}-A_{x})^{2}+(B_{y}-A_{y})^{2}+(B_{z}-A_{z})^{2}}}.$

ผลรวมของสองแรงF 1และF 2 ที่ใช้ที่Aสามารถคำนวณได้จากผลรวมของเซ็กเมนต์ที่กำหนด ให้F 1 = B - AและF 2 = D - Aแล้วผลรวมของเวกเตอร์สองตัวนี้คือ

ฉ=ฉ1+ฉ2=ข-ก+ง-ก,{\ displaystyle \ mathbf {F} = \ mathbf {F} _ {1} + \ mathbf {F} _ {2} = \ mathbf {B} - \ mathbf {A} + \ mathbf {D} - \ mathbf { A},} ${\mathbf {F}}={\mathbf {F}}_{1}+{\mathbf {F}}_{2}={\mathbf {B}}-{\mathbf {A}}+{\mathbf {D}}-{\mathbf {A}},$

ซึ่งสามารถเขียนเป็น

ฉ=ฉ1+ฉ2=2(ข+ง2-ก)=2(จ-ก),{\ displaystyle \ mathbf {F} = \ mathbf {F} _ {1} + \ mathbf {F} _ {2} = 2 ({\ frac {\ mathbf {B} + \ mathbf {D}} {2} } - \ mathbf {A}) = 2 (\ mathbf {E} - \ mathbf {A}),} ${\mathbf {F}}={\mathbf {F}}_{1}+{\mathbf {F}}_{2}=2({\frac {{\mathbf {B}}+{\mathbf {D}}}{2}}-{\mathbf {A}})=2({\mathbf {E}}-{\mathbf {A}}),$

ที่Eเป็นจุดกึ่งกลางของส่วนBDที่ร่วมจุดBและD

ดังนั้นผลรวมของกองกำลังF 1และF 2จึงเป็นสองเท่าของส่วนที่เข้าร่วมAถึงจุดกึ่งกลางEของส่วนที่เข้าร่วมจุดสิ้นสุดBและDของทั้งสองกองกำลัง สองเท่าของความยาวนี้จะประสบความสำเร็จได้อย่างง่ายดายโดยการกำหนดกลุ่มBCและDCขนานไปกับการโฆษณาและABตามลำดับเพื่อให้สี่เหลี่ยมด้านขนานABCD ACเส้นทแยงมุมของรูปสี่เหลี่ยมด้านขนานนี้คือผลรวมของเวกเตอร์แรงทั้งสอง สิ่งนี้เรียกว่ากฎสี่เหลี่ยมด้านขนานสำหรับการเพิ่มกองกำลัง

ชี้กองกำลัง

เมื่อแรงกระทำกับอนุภาคจะถูกนำไปใช้กับจุดเดียว (ปริมาตรของอนุภาคมีค่าเล็กน้อย): นี่คือแรงจุดและอนุภาคคือจุดประยุกต์ของมัน แต่แรงภายนอกที่มีต่อร่างกายที่ขยายออกไป (วัตถุ) สามารถนำไปใช้กับอนุภาคที่เป็นส่วนประกอบจำนวนหนึ่งกล่าวคือสามารถ "แผ่" เหนือปริมาตรหรือพื้นผิวบางส่วนของร่างกายได้ อย่างไรก็ตามการกำหนดเอฟเฟกต์การหมุนที่มีต่อร่างกายนั้นเราต้องระบุจุดที่ใช้งาน (จริงๆแล้วคือสายการใช้งานตามที่อธิบายไว้ด้านล่าง) โดยปกติปัญหาจะได้รับการแก้ไขด้วยวิธีต่อไปนี้:

บ่อยครั้งปริมาตรหรือพื้นผิวที่แรงกระทำมีขนาดค่อนข้างเล็กเมื่อเทียบกับขนาดของร่างกายเพื่อให้สามารถประมาณได้ด้วยจุด โดยปกติจะไม่ยากที่จะระบุว่าข้อผิดพลาดที่เกิดจากการประมาณดังกล่าวเป็นที่ยอมรับได้หรือไม่
หากไม่สามารถยอมรับได้ (อย่างชัดเจนเช่นในกรณีของแรงโน้มถ่วง) แรง "ปริมาตร / พื้นผิว" ดังกล่าวควรถูกอธิบายว่าเป็นระบบของแรง (ส่วนประกอบ) แต่ละตัวกระทำต่ออนุภาคเดียวจากนั้นจึงควรทำการคำนวณสำหรับ แต่ละคนแยกกัน โดยทั่วไปการคำนวณดังกล่าวจะทำให้ง่ายขึ้นโดยใช้องค์ประกอบที่แตกต่างของปริมาตร / พื้นผิวของร่างกายและแคลคูลัสอินทิกรัล ในหลายกรณีสามารถแสดงให้เห็นว่าระบบของกองกำลังดังกล่าวอาจถูกแทนที่ด้วยแรงจุดเดียวโดยไม่ต้องคำนวณจริง (เช่นในกรณีของแรงโน้มถ่วงสม่ำเสมอ)

ไม่ว่าในกรณีใดการวิเคราะห์การเคลื่อนที่ของร่างกายที่แข็งจะเริ่มต้นด้วยแบบจำลองแรงชี้ และเมื่อแสดงแรงที่กระทำต่อร่างกายในรูปแบบกราฟส่วนของเส้นตรงที่เป็นตัวแทนของแรงมักจะถูกวาดเพื่อให้ "เริ่มต้น" (หรือ "สิ้นสุด") ที่จุดสมัคร

ร่างกายแข็ง

ในตัวอย่างที่แสดงในแผนภาพตรงกันข้ามแรงเดี่ยว ฉ→{\ displaystyle \ scriptstyle {\ vec {F}}} $\scriptstyle {\vec F}$ ทำหน้าที่ที่จุดใช้งานHบนร่างกายที่แข็งฟรี ร่างกายมีมวลม{\ displaystyle \ scriptstyle m} $\scriptstyle m$ และศูนย์ของมวลเป็นจุดC ในการประมาณมวลคงที่แรงทำให้เกิดการเปลี่ยนแปลงในการเคลื่อนไหวของร่างกายที่อธิบายโดยนิพจน์ต่อไปนี้:

ก→=ฉ→ม{\ displaystyle {\ vec {a}} = {{\ vec {F}} \ over m}} ${\vec a}={{\vec F} \over m}$ เป็นจุดศูนย์กลางของการเร่งมวล และα→=τ→ผม{\ displaystyle {\ vec {\ alpha}} = {{\ vec {\ tau}} \ over I}} ${\vec \alpha }={{\vec \tau } \over I}$ คือ ความเร่งเชิงมุมของร่างกาย

ในนิพจน์ที่สอง τ→{\ displaystyle \ scriptstyle {\ vec {\ tau}}} $\scriptstyle {\vec \tau }$ คือแรงบิดหรือโมเมนต์ของแรงในขณะที่ผม{\ displaystyle \ scriptstyle I} $\scriptstyle I$ คือช่วงเวลาแห่งความเฉื่อยของร่างกาย แรงบิดที่เกิดจากแรงฉ→{\ displaystyle \ scriptstyle {\ vec {F}}} $\scriptstyle {\vec F}$ เป็นปริมาณเวกเตอร์ที่กำหนดโดยคำนึงถึงจุดอ้างอิงบางจุด:

τ→=ร→×ฉ→{\ displaystyle {\ vec {\ tau}} = {\ vec {r}} \ times {\ vec {F}}} ${\vec \tau }={\vec r}\times {\vec F}$ คือเวกเตอร์แรงบิดและ τ=ฉk{\ displaystyle \ tau = Fk} $\ \tau =Fk$ คือปริมาณแรงบิด

เวกเตอร์ ร→{\ displaystyle \ scriptstyle {\ vec {r}}} $\scriptstyle {\vec r}$ คือเวกเตอร์ตำแหน่งของจุดบังคับและในตัวอย่างนี้วาดจากจุดศูนย์กลางมวลเป็นจุดอ้างอิงของ (ดูแผนภาพ) ส่วนของเส้นตรงk{\ displaystyle \ scriptstyle k} $\scriptstyle k$ คือแขนคันบังคับ ฉ→{\ displaystyle \ scriptstyle {\ vec {F}}} $\scriptstyle {\vec F}$ เกี่ยวกับจุดศูนย์กลางมวล ตามภาพประกอบแนะนำแรงบิดจะไม่เปลี่ยนแปลง (แขนคันบังคับเดียวกัน) หากจุดบังคับเคลื่อนไปตามแนวของการใช้แรง (เส้นประสีดำ) อย่างเป็นทางการมากขึ้นสิ่งนี้ตามมาจากคุณสมบัติของผลิตภัณฑ์เวกเตอร์และแสดงให้เห็นว่าผลการหมุนของแรงขึ้นอยู่กับตำแหน่งของสายการใช้งานเท่านั้นและไม่ได้ขึ้นอยู่กับตัวเลือกเฉพาะของจุดของแอปพลิเคชันตามเส้นนั้น

เวกเตอร์แรงบิดตั้งฉากกับระนาบที่กำหนดโดยแรงและเวกเตอร์ ร→{\ displaystyle \ scriptstyle {\ vec {r}}} $\scriptstyle {\vec r}$ และในตัวอย่างนี้จะมุ่งตรงไปที่ผู้สังเกตการณ์ เวกเตอร์ความเร่งเชิงมุมมีทิศทางเดียวกัน กฎขวามือที่เกี่ยวข้องกับทิศทางนี้ไปตามเข็มนาฬิกาหรือทวนเข็มนาฬิกาหมุนในระนาบของการวาดภาพ

ช่วงเวลาแห่งความเฉื่อย ผม{\ displaystyle \ scriptstyle I} $\scriptstyle I$ คำนวณโดยเทียบกับแกนผ่านจุดศูนย์กลางมวลที่ขนานกับแรงบิด หากร่างกายที่แสดงในภาพประกอบเป็นแผ่นดิสก์ที่เป็นเนื้อเดียวกันช่วงเวลาแห่งความเฉื่อยนี้คือผม=มร2/2{\ displaystyle \ scriptstyle I = mr ^ {2} / 2} $\scriptstyle I=mr^{2}/2$ . หากแผ่นดิสก์มีมวล 0.5 กิโลกรัมและรัศมี 0.8 เมตรโมเมนต์ความเฉื่อยเป็น 0,16 kgm 2 ถ้าจำนวนแรงเท่ากับ 2 N และแขนคันโยก 0,6 ม. แรงบิดเท่ากับ 1,2 Nm ในทันทีที่แสดงแรงจะทำให้ดิสก์มีความเร่งเชิงมุมα = τ / I = 7,5 rad / s 2และที่จุดศูนย์กลางมวลจะให้ความเร่งเชิงเส้น a = F / m = 4 m / s 2 .

การวางแบบกราฟิกของแรงผลลัพธ์

แรงและแรงบิดที่เป็นผลลัพธ์จะแทนที่ผลกระทบของระบบแรงที่กระทำต่อการเคลื่อนไหวของร่างกายที่แข็ง กรณีพิเศษที่น่าสนใจคือผลลัพธ์ที่ปราศจากแรงบิดซึ่งสามารถพบได้ดังต่อไปนี้:

เวกเตอร์นอกจากนี้ใช้ในการหาแรงสุทธิ
ใช้สมการเพื่อกำหนดจุดที่มีแรงบิดเป็นศูนย์:

ร→×ฉ→ร=∑ผม=1น(ร→ผม×ฉ→ผม){\ displaystyle {\ vec {r}} \ times {\ vec {F}} _ {\ mathrm {R}} = \ sum _ {i = 1} ^ {N} ({\ vec {r}} _ { i} \ times {\ vec {F}} _ {i})} ${\vec {r}}\times {\vec {F}}_{\mathrm {R} }=\sum _{i=1}^{N}({\vec {r}}_{i}\times {\vec {F}}_{i})$

ที่ไหน ฉ→ร{\ displaystyle {\ vec {F}} _ {\ mathrm {R}}} ${\vec {F}}_{\mathrm {R} }$ คือแรงสุทธิ ร→{\ displaystyle {\ vec {r}}} ${\vec {r}}$ ระบุตำแหน่งของจุดสมัครและกองกำลังส่วนบุคคลคือ ฉ→ผม{\ displaystyle {\ vec {F}} _ {i}} ${\vec {F}}_{i}$ พร้อมคะแนนแอปพลิเคชัน ร→ผม{\ displaystyle {\ vec {r}} _ {i}} ${\vec {r}}_{i}$ . อาจเป็นไปได้ว่าไม่มีจุดใดของการใช้งานที่ให้ผลลัพธ์ที่ปราศจากแรงบิด

แผนภาพตรงข้ามแสดงให้เห็นถึงวิธีการแบบกราฟิกอย่างง่ายสำหรับการค้นหาแนวการประยุกต์ใช้แรงที่เป็นผลลัพธ์ของระบบระนาบอย่างง่าย:

แนวการประยุกต์ใช้กองกำลังจริง ฉ→1{\ displaystyle {\ vec {F}} _ {1}} ${\vec {F}}_{1}$ และ ฉ→2{\ displaystyle {\ vec {F}} _ {2}} ${\vec {F}}_{2}$ ทางด้านซ้ายสุดของภาพประกอบตัดกัน หลังจากดำเนินการเพิ่มเวกเตอร์แล้ว "ที่ตำแหน่งของฉ→1{\ displaystyle {\ vec {F}} _ {1}} ${\vec {F}}_{1}$ "แรงสุทธิที่ได้รับจะถูกแปลเพื่อให้สายการใช้งานผ่านจุดตัดร่วมในส่วนที่เกี่ยวกับจุดนั้นแรงบิดทั้งหมดจึงเป็นศูนย์ดังนั้นแรงบิดของแรงผลลัพธ์ ฉ→ร{\ displaystyle {\ vec {F}} _ {\ mathrm {R}}} ${\vec {F}}_{\mathrm {R} }$ เท่ากับผลรวมของแรงบิดของกองกำลังจริง
ภาพประกอบตรงกลางของแผนภาพแสดงแรงจริงสองแรงขนานกัน หลังจากบวกเวกเตอร์ "ที่ตำแหน่งของฉ→2{\ displaystyle {\ vec {F}} _ {2}} ${\vec {F}}_{2}$ "แรงสุทธิจะถูกแปลเป็นบรรทัดการใช้งานที่เหมาะสมโดยที่มันจะกลายเป็นแรงผลลัพธ์ ฉ→ร{\ displaystyle \ scriptstyle {\ vec {F}} _ {\ mathrm {R}}} $\scriptstyle {\vec {F}}_{\mathrm {R} }$ . ขั้นตอนนี้ขึ้นอยู่กับการสลายตัวของกองกำลังทั้งหมดเป็นส่วนประกอบที่เส้นของการใช้งาน (เส้นประสีซีด) ตัดกัน ณ จุดหนึ่ง (เสาที่เรียกว่าตั้งค่าโดยพลการที่ด้านขวาของภาพประกอบ) จากนั้นอาร์กิวเมนต์จากกรณีก่อนหน้าจะถูกนำไปใช้กับกองกำลังและส่วนประกอบเพื่อแสดงความสัมพันธ์ของแรงบิด
ขวาสุดแสดงภาพประกอบคู่ , กองทัพทั้งสองเท่ากัน แต่ตรงข้ามที่ปริมาณของแรงสุทธิเป็นศูนย์ แต่พวกเขาผลิตแรงบิดสุทธิτ=ฉง{\ displaystyle \ scriptstyle \ tau = Fd} $\scriptstyle \tau = Fd$ ที่ไหน ง{\ displaystyle \ scriptstyle \ d} $\scriptstyle \ d$ คือระยะห่างระหว่างบรรทัดการสมัคร เนื่องจากไม่มีแรงที่เป็นผลลัพธ์แรงบิดนี้จึงสามารถ [คือ?] อธิบายได้ว่าเป็นแรงบิด "บริสุทธิ์"

แผนภาพเวกเตอร์สำหรับการเพิ่มแรงที่ไม่ขนานกัน

โดยทั่วไประบบของกองกำลังที่กระทำต่อร่างกายที่แข็งสามารถถูกแทนที่ได้ด้วยแรงเดียวกับแรงบิดบริสุทธิ์หนึ่งตัว (ดูหัวข้อก่อนหน้า) แรงคือแรงสุทธิ แต่ในการคำนวณแรงบิดเพิ่มเติมต้องกำหนดแรงสุทธิให้กับแนวปฏิบัติ สามารถเลือกแนวการกระทำได้ตามอำเภอใจ แต่แรงบิดบริสุทธิ์เพิ่มเติมขึ้นอยู่กับตัวเลือกนี้ ในกรณีพิเศษมันเป็นไปได้ที่จะพบว่าแรงบิดที่เพิ่มขึ้นนี้เป็นศูนย์

แรงลัพธ์และแรงบิดสามารถกำหนดสำหรับการกำหนดค่าของกองกำลังใด ๆ อย่างไรก็ตามกรณีพิเศษที่น่าสนใจคือผลลัพธ์ที่ปราศจากแรงบิด สิ่งนี้มีประโยชน์ทั้งในเชิงแนวคิดและในทางปฏิบัติเนื่องจากร่างกายเคลื่อนไหวโดยไม่หมุนราวกับว่าเป็นอนุภาค